Avec le développement des techniques d’affinement en IA (RAG, fine-tuning) pour adapter les modèles à nos besoins spécifiques, il peut être important de s’intéresser à une notion fondamentale : les embeddings.
Ils permettent de représenter des données (texte, image, son…) sous forme vectorielle compréhensible et exploitable par les modèles IA, en particulier les LLMs qui s’appuient sur de grandes quantités de données. Dans cet article, nous verrons, à travers un exemple concret, le processus de transformation d’un texte en vecteurs. Nous allons, à l’aide d’une base de données vectorielle ChromaDB, stocker et interroger des embeddings, en utilisant des outils open-source comme LangChain et Ollama.
Transformation des données en embeddings
Comme mentionné dans l’introduction, les modèles ont besoin de représentations numériques pour comprendre et pouvoir traiter les données. Avant d’aller plus loin, nous allons d’abord essayer de comprendre la notion mathématique de tenseurs qui constitue la base de ces représentations vectorielles.
1. Les tenseurs
Il faut voir un tenseur comme une structure de données (un tableau) qui généralise les notions de vecteur et de matrice à des dimensions supérieures.
Un tenseur se caractérise par sa dimension, qui correspond au nombre d’indices nécessaires pour accéder à un élément du tableau, et par sa taille, qui indique le nombre d’éléments dans chaque dimension.
Exemples :
\(V = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\) est un tenseur de dimension 1 (1-tenseur), de taille (3,)
\(M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}\) est un tenseur de dimension 2 (2-tenseur), de taille (2, 3)
\(T = \begin{pmatrix} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \\ \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} \end{pmatrix}\) est un tenseur de dimension 3 (3-tenseur), de taille (2, 2, 2)
En programmation, il est facile de créer et de manipuler des tenseurs à l’aide des bibliothèques Python comme NumPy ou TensorFlow. Le code suivant permet par exemple de représenter nos trois tenseurs ci-dessus à l’aide de Numpy :
import numpy as np
V = np.array([1, 2, 3])
M = np.array([[1, 2, 3], [4, 5, 6]])
T = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("Tenseur V => Dimension :", V.ndim, "| Taille :", V.shape)
print("Tenseur M => Dimension :", M.ndim, "| Taille :", M.shape)
print("Tenseur T => Dimension :", T.ndim, "| Taille :", T.shape)
Le résultat obtenu correspond bien à la sortie attendue :
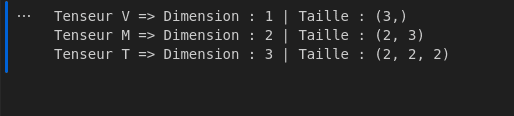
Cette généralisation qu’offre les tenseurs permet de représenter facilement des données multidimensionnelles, ce qui est important mais nous avons aussi besoin que ces représentations vectorielles puissent aussi capturer la signification sémantique des données brutes transformées => ce qui nous conduit à la notion d’embeddings.
2. Les embeddings
Ce sont des représentations vectorielles des données brutes dans un espace où les relations sémantiques entre les données sont conservées. Les données ayant une signification proche auront des vecteurs proches (cf. la page wikipédia dédiée au modèle vectoriel pour plus de détails). Cette relation entre les données est quantifiée par des mesures de similarité. Une de ces mesures est la similarité cosinus qui se base sur le calcul du cosinus entre deux vecteurs par la formule suivante :
\(cos(\theta) = \frac{V \cdot W}{\|V\| \|W\|}\)
où :
– \(V \cdot W\) est le produit scalaire entre les deux vecteurs
– \(\|V\|\) et \(\|W\|\) les normes des deux vecteurs
Dans un repère orthonormal, il est facile de constater que plus \(cos(\theta)\) est proche de 1, plus les vecteurs sont proches donc similaires.
La transformation des données brutes en embeddings est faite grâce à des modèles d’embeddings tels que Word2Vec, nomic-embed-text…
Base de données vectorielle et recherche d’informations
Une base de données vectorielle, comme son nom l’indique, est une base de données qui stocke des représentations vectorielles (embeddings) et permet d’effectuer des recherches en mesurant la similarité entre ces vecteurs.
Nous allons maintenant voir un cas pratique de transformation d’un texte en embeddings ainsi que le stockage et le requêtage des embeddings. Le texte suivant est utilisé comme base de connaissances :
La recherche d'information (RI) est le domaine qui étudie la manière de retrouver des informations dans un corpus.
Celui-ci est composé de documents d'une ou plusieurs bases de données, qui sont décrits par un contenu ou les métadonnées associées.
Le modèle vectoriel est une représentation mathématique du contenu d'un document, selon une approche algébrique.
En introduisant des mesures de similarité adaptées, on peut quantifier la proximité sémantique entre différents documents.
Les mesures de similarité sont choisies en fonction de l'application. Une mesure très utilisée est la similarité cosinus.
Et nous allons interroger la base avec les deux questions suivantes :
1. C'est quoi a recherche d'information (RI) ?
2. Quelle mesure de similarité est très utilisée ?
Pour cela, il faut d’abord installer Ollama et récupérer le modèle nomic-embed-text en local en exécutant la commande :
ollama pull nomic-embed-text
Ensuite, nous installons les dépendances Python nécessaires :
pip install langchain langchain_ollama langchain_chroma
LangChain est un framework puissant qui simplifie le développement d’applications basées sur les LLMs. Pour plus de détails sur les fonctionnalités de LangChain, consultez la documentation.
Avant de stocker les données, nous avons besoin de segmenter le texte en petits morceaux (chunks). Par ailleurs, il faut à la base de données une fonction d’embedding pour pouvoir convertir les chunks en vecteurs.
from langchain_text_splitters import RecursiveCharacterTextSplitter
from langchain_ollama import OllamaEmbeddings
from langchain.schema import Document
def split_text_into_documents(text):
documents = []
text_splitter = RecursiveCharacterTextSplitter(
chunk_size=100,
chunk_overlap=30,
separators=["\n"]
)
chunks = text_splitter.split_text(text)
for i, chunk in enumerate(chunks):
doc = Document(page_content=chunk, metadata={"source": f"chunk_{i}"})
documents.append(doc)
return documents
def get_embedding_function():
return OllamaEmbeddings(model="nomic-embed-text")
Après l’étape de préparation du texte et de la fonction d’embedding, nous passons au stockage dans la base ChromaDB et à la fonction de recherche.
Il est important de noter que ChromaDB utilise par défaut la distance euclidienne (L2 Distance) comme mesure de similarité. Un score faible (proche de 0) indique une réponse très pertinente.
from langchain_chroma import Chroma
def store_embeddings(documents, embedding_model):
vector_db = Chroma(
persist_directory='./chroma_db', embedding_function=embedding_model
)
vector_db.add_documents(documents)
return vector_db
def query_vector_db(question, vector_db):
results = vector_db.similarity_search_with_score(question, k=1)
print(f"Question: {question}")
for doc, score in results:
print(f"Réponse (score: {score:.2f}) : {doc.page_content}\n")
Nous pouvons à présent tester la base de données vectorielle en effectuant une requête.
from embedding_generator import split_text_into_documents, get_embedding_function
from vector_store import store_embeddings
from vector_query import query_vector_db
text = """La recherche d'information (RI) est le domaine qui étudie la manière de retrouver des informations dans un corpus.
Celui-ci est composé de documents d'une ou plusieurs bases de données, qui sont décrits par un contenu ou les métadonnées associées.
Le modèle vectoriel est une représentation mathématique du contenu d'un document, selon une approche algébrique.
En introduisant des mesures de similarité adaptées, on peut quantifier la proximité sémantique entre différents documents.
Les mesures de similarité sont choisies en fonction de l'application. Une mesure très utilisée est la similarité cosinus."""
documents = split_text_into_documents(text)
vector_db = store_embeddings(documents, get_embedding_function())
questions = [
"C'est quoi a recherche d'information (RI) ?",
"Quelle mesure de similarité est très utilisée ?"
]
for question in questions:
query_vector_db(question, vector_db)
Nous obtenons le résultat suivant :

Comme nous pouvons le constater, le score 0.28 montre que les réponses obtenues sont pertinentes.
Les embeddings sont au cœur des modèles d’IA modernes, permettant de représenter et de manipuler efficacement des données textuelles. En utilisant LangChain, nous avons illustré comment transformer du texte en embeddings, les stocker dans une base vectorielle et interroger cette base pour obtenir des réponses pertinentes.
Ces réponses pertinentes peuvent être fournies en tant que context aux LLMs pour former un système de RAG (technique très en vogue et très utilisée ces temps-ci).